The Coronavirus (COVID-19) is spreading all over the world. The contagion that started in Wuhan city has now expanded to Italy, Iran, and many other countries. It has become more than just an “Asian” virus; it is an Italian virus, Iranian virus, and so on.

It seems that being positive or negative for coronavirus is all that people care about. The test referred to here is called the Polymerase Chain Reaction (PCR) test. This method enables analysis of specific DNA sequences by amplifying DNA or RNA copies from a sample. It has become such a fundamental technology for any molecular biology and genetic engineering science. Dr. Kary Mullis, who invented this method, was awarded the Nobel Prize in 1993 for this accomplishment.

The public urges officials to increase the capacity for conducting more PCR tests in order to identify coronavirus cases, but frankly, I wonder how meaningful that would be. People say that they want assurance, but I personally feel that there would be no assurance whatsoever through this test. The RT-PCR (Reverse Transcription PCR) test is not even perfect, and thus won’t be able to detect cases with 100% certainty. The instant test kit would be even less reliable.
Let’s do some simulation using the Diamond Princess cruise ship incident, or as some might call it, “the floating Wuhan”, as an example. Based on the official data as of February 18, let’s assume that the total population of the cruise ship was 3,700.

And let’s also assume that the RT-PCR test had a very high detection accuracy of:
- Sensitivity (i.e. the probability to correctly identify 95 positive cases out of 100 positive samples): 95 percent
- Specificity (i.e. the probability to correctly identify 95 negative cases out of 100 negative samples): 95 percent
Assuming as such, the RT-PCR test can be considered highly valid.
According to the Nikkei, 1,723 people on the cruise ship were tested, out of which 454 were diagnosed coronavirus positive; thus, the percentage of disease carriers is about 26%. Based on this data, we now consider a hypothetical situation where all passengers had been tested.
- Estimated positive cases: 3,700*0.26 = 962
- Estimated negative cases: 3,700 – 962 = 2,738
- The
total number of cases that would be identified as positive (through RT-PCR
test):
- True positive cases: 962*0.95 = 914
- Cases falsely identified as positive: 2,738*0.05 = 137
- The
total number of cases that would be identified as negative (through RT-PCR
test):
- True negative cases: 2,738*0.95 = 2,601
- Cases falsely identified as negative: 962*0.05 = 48
It is quite possible to have a case where someone who is identified as negative was actually a carrier (false negative). This is even when using a valid test.
Let’s now extend this hypothetical simulation to the national level in Japan. Let’s assume that there were 100,000 people infected (remember, this is just hypothetical). To make the calculation easier, we set the total population of the country at 120 million. Then, the prevalence rate would be 0.08%. Assuming the same sensitivity and specificity of the PCR test, that is, 95%, what is the probability of a randomly picked person among those who tested positive to be a true positive carrier?
This can be computed using Bayes’ theorem which is a formula to solve simple conditional probability questions.

- The infected population: 0.1 million
- The non-infected population: 119.9 million
- The
total number of people who would be identified as positive:
- True positive cases: 0.1 million*0.95 = 95,000
- People falsely identified as positive: 119.9 million*0.05 = 5.995 million
- The
total number of people who would be identified as negative:
- True negative cases: 119.9 million*0.95 = 113.905 million
- People falsely identified as negative: 0.1 million*0.05 = 5,000
Thus, the probability of a positively identified person to be a real coronavirus carrier is: 95,000/(95,000 + 5,995,000) = 1.6%
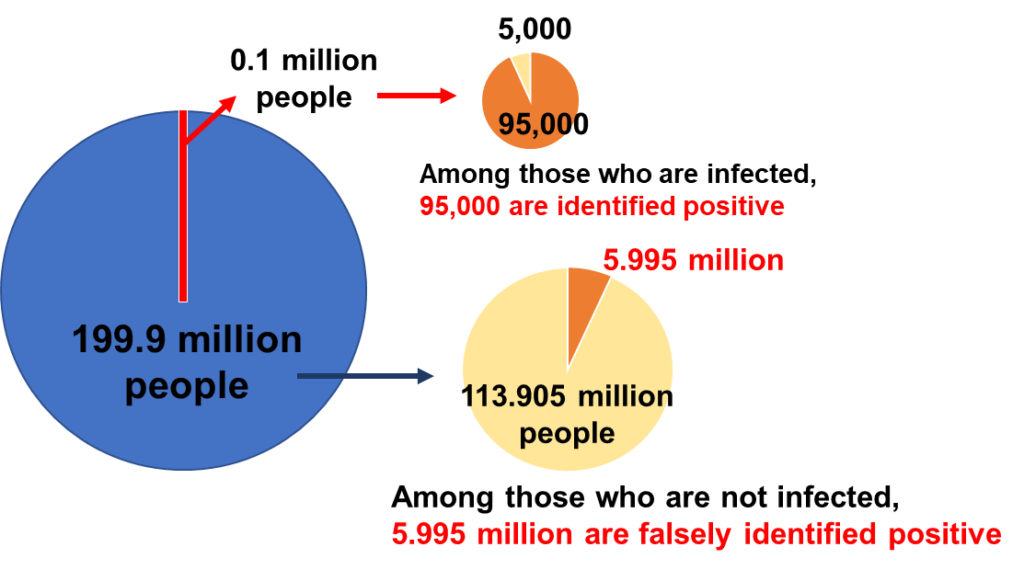
If we were to randomly pick a person from the positively tested population pool, the probability that the person is actually truly positive is 1.6%, and this is under the assumption that the PCR test was highly capable of detecting coronavirus.
What can be deduced from the above is:
- It is imperative to put priority on testing people who are likely to show positive results; and
- In the end, the truth is very hard to see and hard to confirm by a test, so putting every effort for disease control and preventive measures is more important than making sure everyone gets tested.
This virus is different from a general flu, and its characteristics are still largely unknown. Therefore, there is a need to take an exhaustive approach to fight against the worsening situation. An unusual level of caution should be applied because this is not something we are familiar with; what we are dealing with is an unknown. The test results are simply one indicator to grasp the overall picture. What we know so far is that the elderly population has a higher mortality rate that goes beyond 10%. We shouldn’t just be shouting that testing is necessary; the important things we need to collectively focus on right now are to make sure we maintain a functional medical infrastructure, as well as quarantine those who are potentially infected.
Reference: https://www.gohongi-clinic.com/k_blog/3873/